전자회로의 기초는 저항과 전압원(배터리)로 이뤄진 회로에서 시작하며, 이 회로에서 전압과 전류의 값을 계산하는 것이 중요합니다.
전압과 전류가 무엇이며, 저항은 또 뭐고 전압원이 뭔지 모르는 분들도 계실 것이라 생각됩니다. 각각의 개념에 대한 글은 차차 작성하고 있으며, 글자를 클릭하면 해당 글로 이동됩니다.
키르히호프 법칙
회로에서 전압과 전류의 값을 얻는 과정을 '회로를 해석한다'라고 합니다. 키르히호프 법칙은 회로를 해석하는 가장 중요한 방법이며, 가장 기초가 되는 법칙입니다.
키르히호프 법칙에는 두 가지가 있습니다.
키르히호프의 전류 법칙 (KCL)
키르히호프의 전압 법칙 (KVL)
KCL (키르히호프의 전류 법칙)
키르히호프의 전류 법칙 (KCL)은 전류에 대한 법칙으로 회로에서 전류의 흐름을 파악하는데 필수인 법칙입니다.
이 법칙은 다음과 같습니다.
회로의 한 점으로 들어가고, 나가는 전류의 합은 동일하다.
회로의 어떤 한 점에 10A가 들어가면, 나가는 전류는 10A가 되어야한다는 뜻입니다.
수식으로는 (나가는 전류) = (들어가는 전류)로 쓸 수 있습니다. 또는 (나가는 전류) - (들어가는 전류) = 0으로 쓸 수도 있죠.
(나가고 들어가는 전류의 총 합) = 0으로 쓸 수도 있습니다. 다음 그림을 보면 이해가 될 것입니다.

여기서 한 점이라고 언급했지만, "연결된 지점"이라고 이해하시면 됩니다. 위의 그림에서 KCL을 적용해 보면,
(들어가는 전류) = (나가는 전류)에서
4+4+(-1)+(-7) = 0으로 쓸 수 있습니다.
여기서 -1A, -7A은 음수이기 때문에 실제로는 위의 그림과 반대 방향으로 전기가 흐른다고 생각하시면 됩니다.
KVL (키르히호프의 전압 법칙)
전류를 해석하는데 KCL를 사용했다면, 전압을 설명하는데 KVL을 사용합니다. 사실 둘은 한 회로를 해석하는데 있어 모두 사용되어야 하는 법칙이죠.
KVL은 다음과 같습니다.
한 닫힌 루프 내에서 전압의 총합은 0이다.
여기서 닫힌 루프란 끊어지지 않은 회로를 의미합니다.
아래의 사진은 닫힌 루프의 한 종류입니다.

아래의 그림은 닫힌 루프가 아닙니다.

키르히호프의 전압 법칙 (KVL)은 닫힌 루프 내에서만 적용되는 법칙입니다.
KVL은 닫힌 루프 내의 총 전압이 0이라고 했는데, 이는 다음과 같이 쓸 수도 있습니다.
(공급하는 전압) = (소비되는 전압)
위의 닫힌 루프를 좀 더 정확하게 그려보겠습니다.
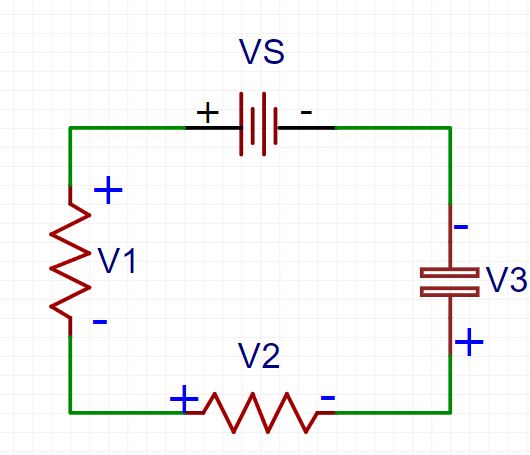
극성을 그려봤습니다. 이제 이 회로에 KCL을 적용해보겠습니다.
VS = V1 + V2 + V3
여기서 VS는 배터리의 전압이기 때문에 공급하는 전압, V1 ~ 3는 전기 에너지를 소비하는 소자들이기 때문에 소비하는 전압이라고 생각할 수 있습니다.
여기서는 VS가 배터리 기호를 사용하기 때문에 공급하는 전압이라고 여길 수 있었습니다. 하지만, 세상에는 이것이 어떤 것이 전압을 공급하고, 소비하는지 모르는 경우가 허다합니다.
이 때는 임의로 모든 소자의 극성을 임의로 지정하고, 반시계방향으로 회로를 따라갈 때, - -> +로 극성이 변하는 것은 공급, + -> -로 변하는 것은 소비로 생각하시면 됩니다.
위의 회로에선 VS가 반시계방향으로 회로를 볼 때, - -> +로 부호가 변했으니, 공급원으로 볼 수 있습니다.
극성은 정해진 것이 아니고, 여러분들이 임의로 부여하면 되는 것이며, 극성이 다르다고 해서 회로의 해석이 달라지는 것은 아님을 명심하시기를 바랍니다. 예를 들어 위의 회로는 아래과 같이 그릴 수도 있습니다.
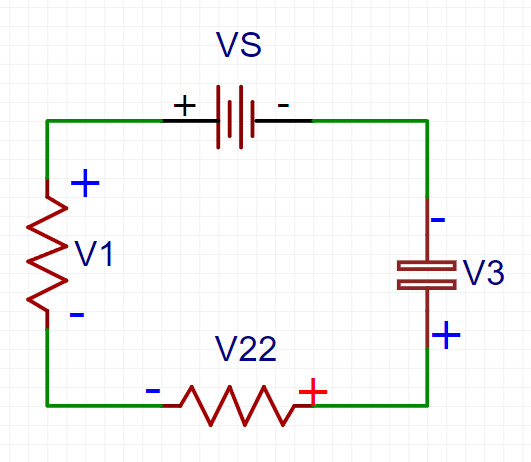
첫 번째 회로와 비교했을 때, 가운데 저항의 극성이 바뀐 것을 확인할 수 있습니다.
여기서 KVL을 구하고, 공급원과 소비원을 나누면 다음과 같습니다.
| 공급원 | 소비원 |
| - -> + | + -> - |
| VS | V1 |
| V22 | V3 |
여기서 V22를 공급원이라 가정했다고 해도, 실제로 공급원인지 아닌지는 식을 풀어야 알 수 있습니다.
방정식을 세우면 다음과 같습니다.
VS + V22 = V1 + V3
결론
KVL과 KCL은 회로를 해석하는데 있어 거의 항상 사용되는 법칙입니다.
간단하기 때문에 간과할 수도 있지만, 모든 해석의 기초가 되는 법칙이기 때문에 항상 명심하고 있어야 합니다.
다음은 합성 저항과 저항에 따른 전압 분배, 전류 분배에 대해 알아보겠습니다.
'전자회로 > 전자회로 ko' 카테고리의 다른 글
| 전자회로 00. 시작 (0) | 2022.04.18 |
|---|
